视频加载中...
3.5「高数帮」深度解析,定积分的核心理念与关键性质
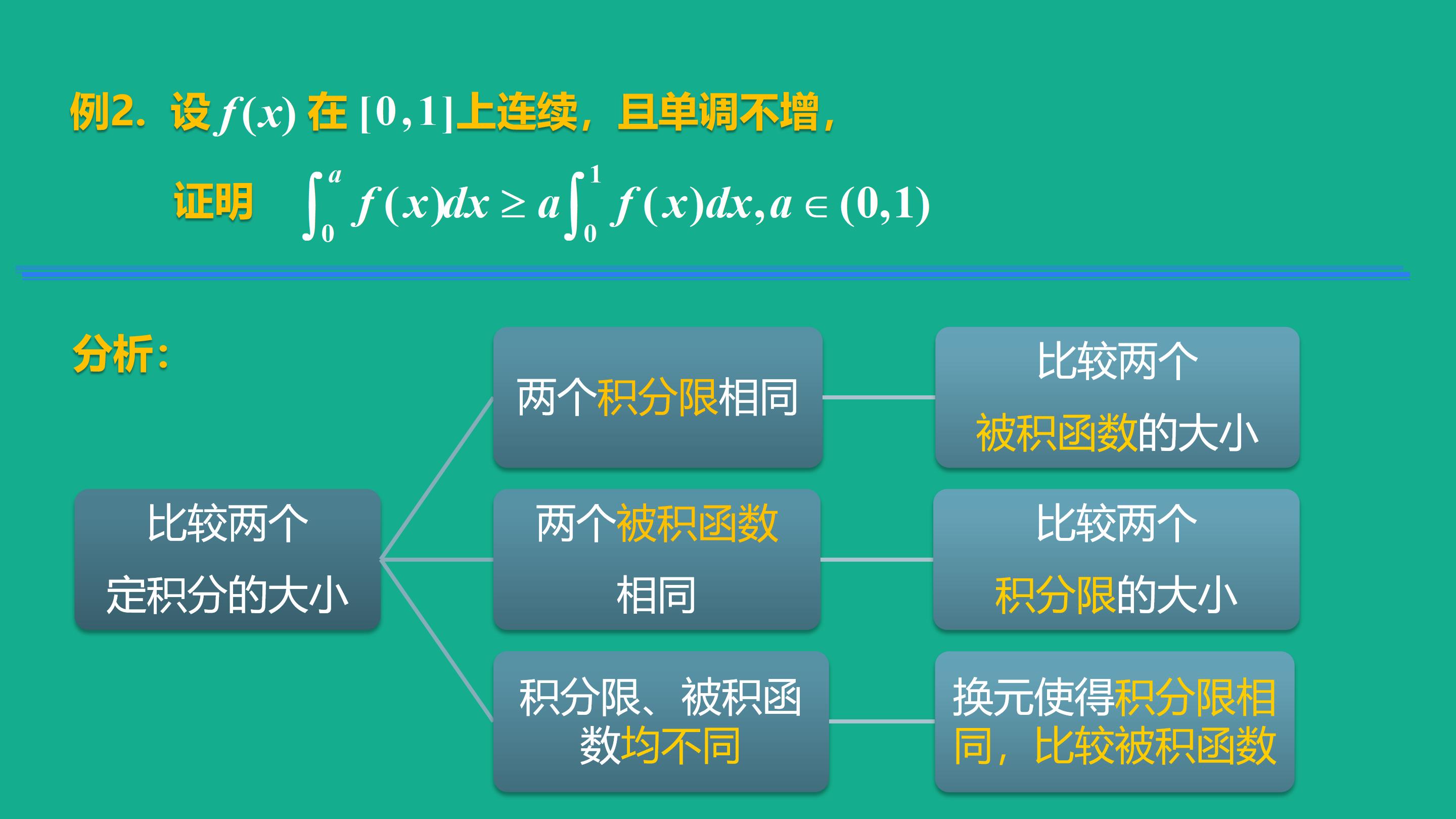
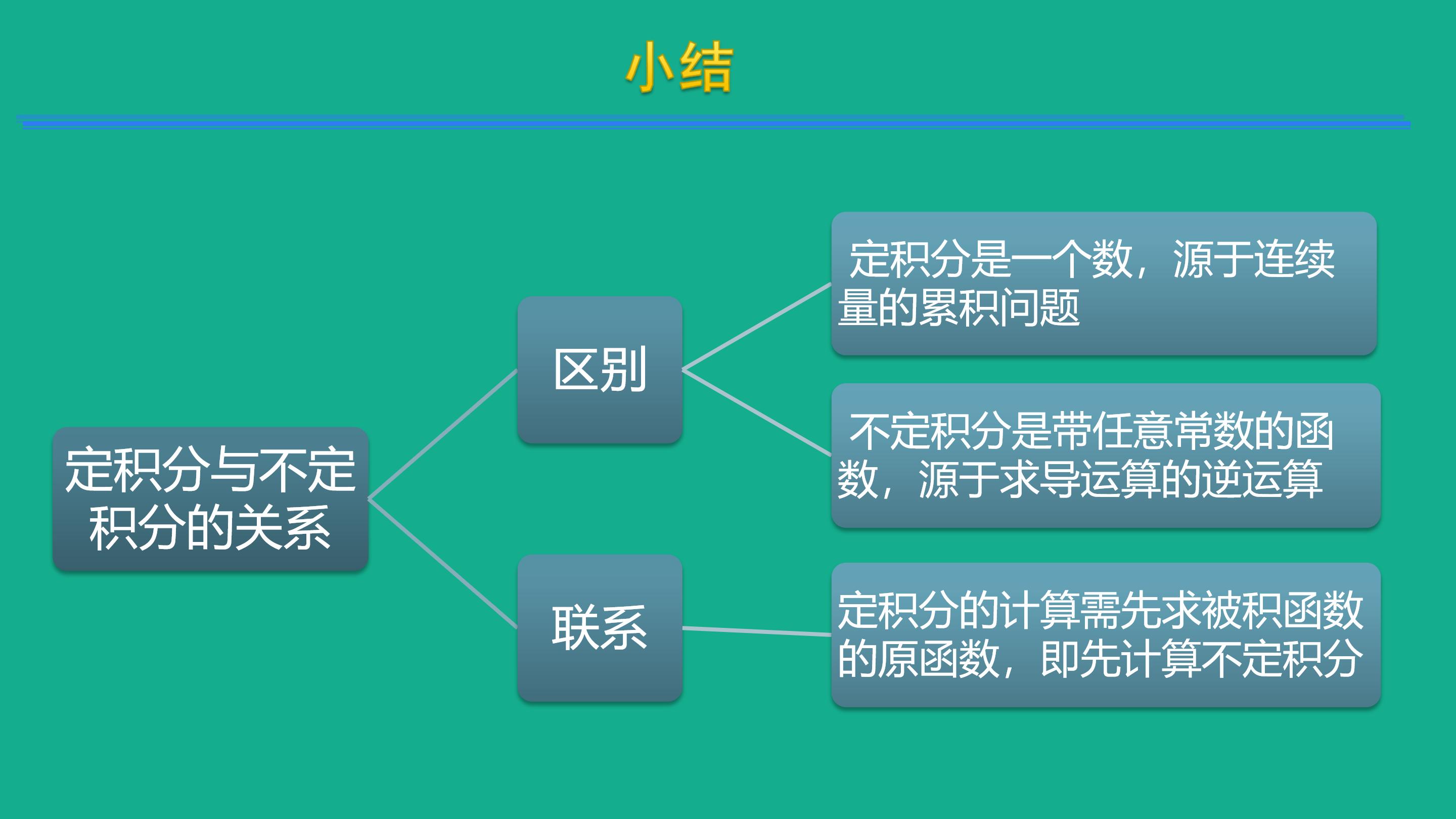
定积分是微积分学中的一个基本概念，它用于计算一个函数在一个区间上的累积效应。以下是定积分的概念和性质：
### 定积分的概念
定积分可以理解为在几何上表示曲线下（或上）与x轴围成的面积，在物理上表示力在一段距离上的累积做功，在经济学上表示收益或成本在一段时间内的累积等。
"定义"：设函数f(x)在闭区间[a, b]上连续，将区间[a, b]分成n个小区间，每个小区间的长度为Δx，在每个小区间上取一点ξ（a ≤ ξ ≤ b），构造和式：
S = f(ξ1)Δx + f(ξ2)Δx + ... + f(ξn)Δx
当n趋向于无穷大，且每个小区间的长度Δx趋向于0时，这个和式的极限如果存在，就称这个极限为函数f(x)在区间[a, b]上的定积分，记作：
∫[a, b] f(x) dx
### 定积分的性质
1. "线性性质"：
- ∫[a, b] (cf(x) + g(x)) dx = c∫[a, b] f(x) dx + ∫[a, b] g(x) dx，其中c是常数。
2. "区间可加性"：
- 如果
相关内容：
1