牛顿(Isaac Newton,1643年1月4日—1727年3月31日)是英国著名的物理学家、数学家和天文学家,被广泛认为是历史上最伟大的科学家之一。以下是关于牛顿的一些重要信息:
1. "科学贡献":
- "牛顿运动定律":提出了描述物体运动的基本定律,奠定了经典力学的基础。
- "万有引力定律":揭示了所有物体之间都存在相互吸引的力,并提出了万有引力定律。
- "微积分":与莱布尼茨共同发明了微积分,为数学分析奠定了基础。
- "光学研究":对光的折射和反射进行了深入研究,提出了光的粒子说。
2. "生平":
- 牛顿出生于英国林肯郡的一个农民家庭,自幼对自然科学充满兴趣。
- 1661年,牛顿进入剑桥大学学习,1665年因瘟疫爆发回到家乡,在此期间开始进行科学研究。
- 1667年,牛顿重返剑桥大学,并成为该校教授。
- 1687年,牛顿发表了著名的《自然哲学的数学原理》,系统地阐述了牛顿运动定律和万有引力定律。
- 1703年,牛顿当选为英国皇家学会会长。
3. "影响":
- 牛顿的科学研究对后世产生了深远的影响,为物理学、数学、天文学等领域的发展奠定了基础。
- 牛顿的成就被誉为“
定积分的定义。
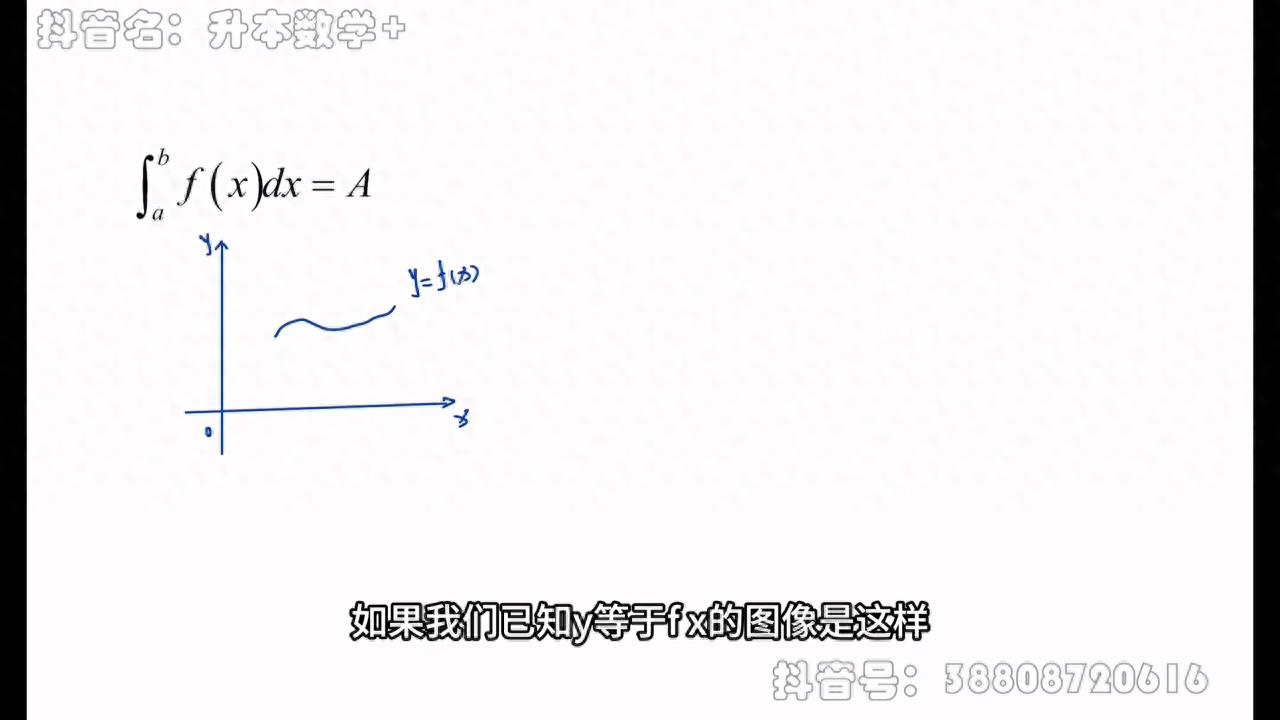
我们来简单学习一下定积分的定义。大家可以看到定积分形式上其实就是不定积分,多了上下限,它可以计算出来等于一个常数a,我们可以用图像来理解一下它。
如果我们已知y等于fx的图像是这样,它与x轴围成的一块曲边图形,我们去计算这个图形的面积。由于图形的一边是曲线,我们没办法使用矩形的面积计算公式,但是我们可以使用微元法,就是将这个图形划分为无数个像这样的小矩形。
只要我们划分的足够小,上边的曲线就可以近似的看作一条小直线,而这个矩形的宽,我们可以把它看作DX。长其实就是我们函数y的函数值,也即是我们的fx,从而一个小矩形的面积,就是等于fx乘以dx。整个曲边图形的面积,就等于把这所有的小矩形累加起来,也就是a到bfx的定积分,这样去无限切分这个图形的思想。
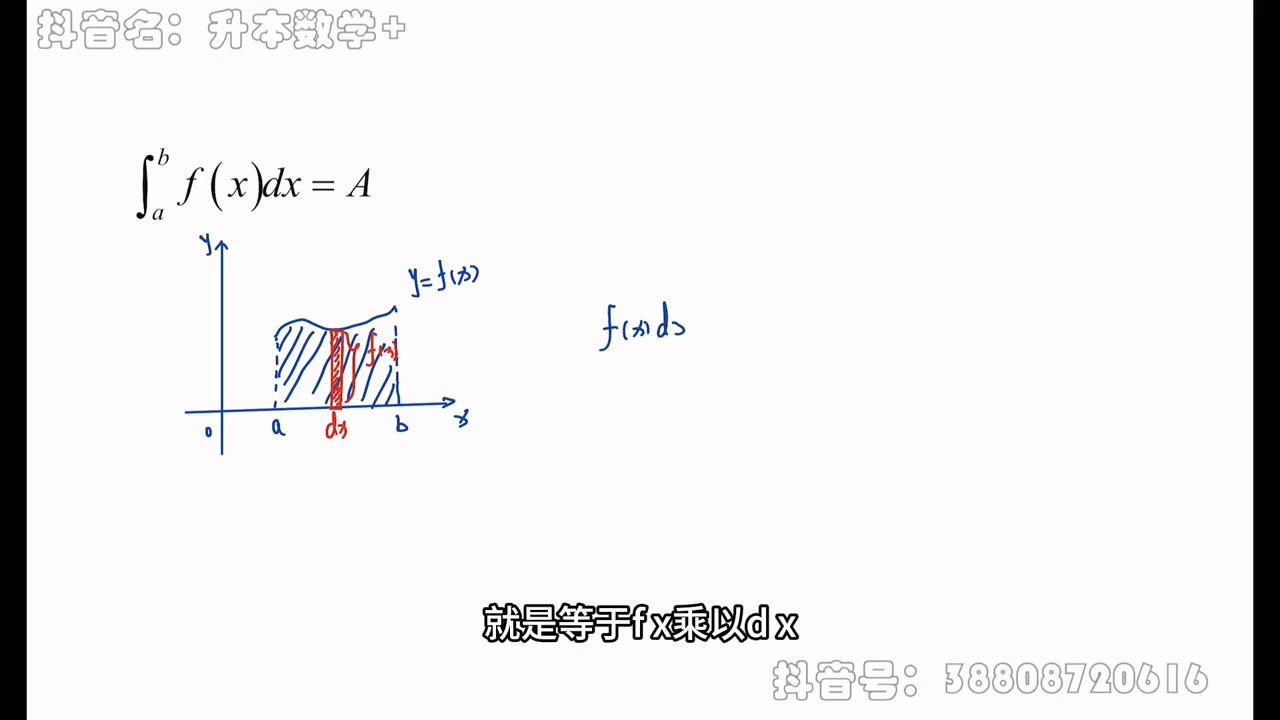
这就是我们的微元法,也可以看作是极限的思想,因为我们切的矩形要足够多,就是取极限。而大家还得注意的是,如果函数推向在x轴下边,那么你可以得到的是fx的值就为负,定积分你算出来它就为负数。总之大家得知道定积分是一个数。
以上就是定积分的定义的简单描述,请持续关注,接下来会给大家讲解牛顿-莱布尼茨公式。


