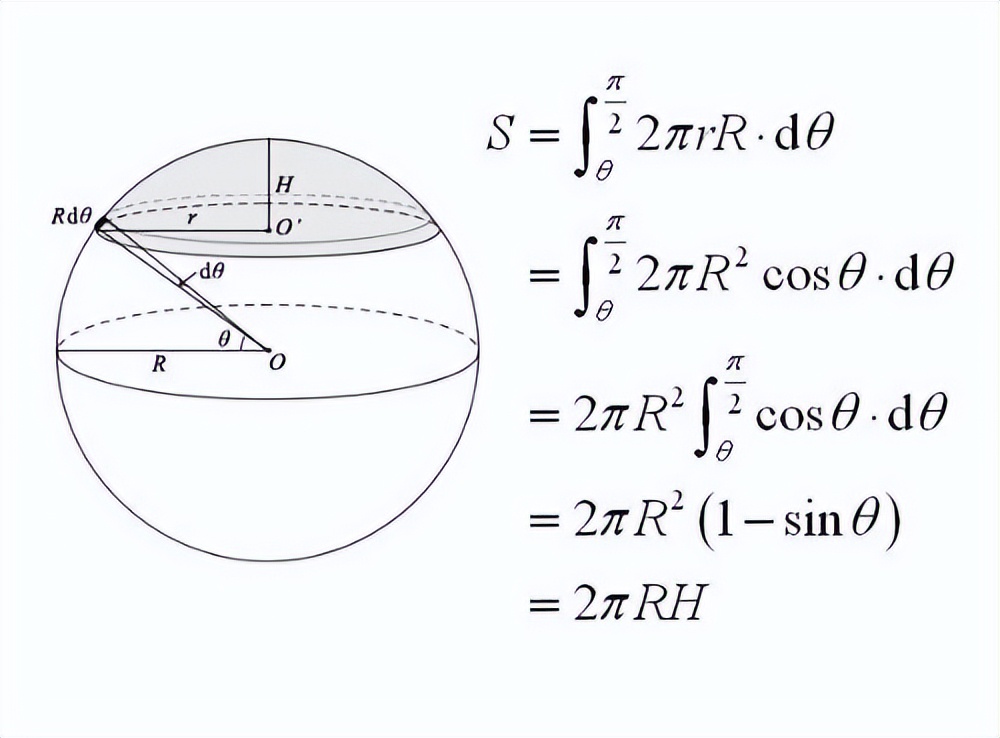
你开门见山地问道:定积分是什么呢?
我答道:不要着急,先让我讲个故事,再告诉你也不迟。
在很久很久以前,人们不会精确地去算曲线围成的面积,只是用各种巧妙的方法进行近似的估算。(大家不要认为前人没有微积分就估不出面积,数学源于智慧,智慧却不止步于数学)

据说阿基米德早于牛顿和莱布尼兹研究出了积分,不过阿基米德的方法年代过于久远已无从考证,不知道那究竟是真是假了。

阿基米德

阿基米德螺线
后来牛顿和莱布尼兹发明了微积分,给出了这个公式,极大地简化了人们对曲边图形面积的估算。

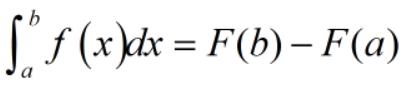
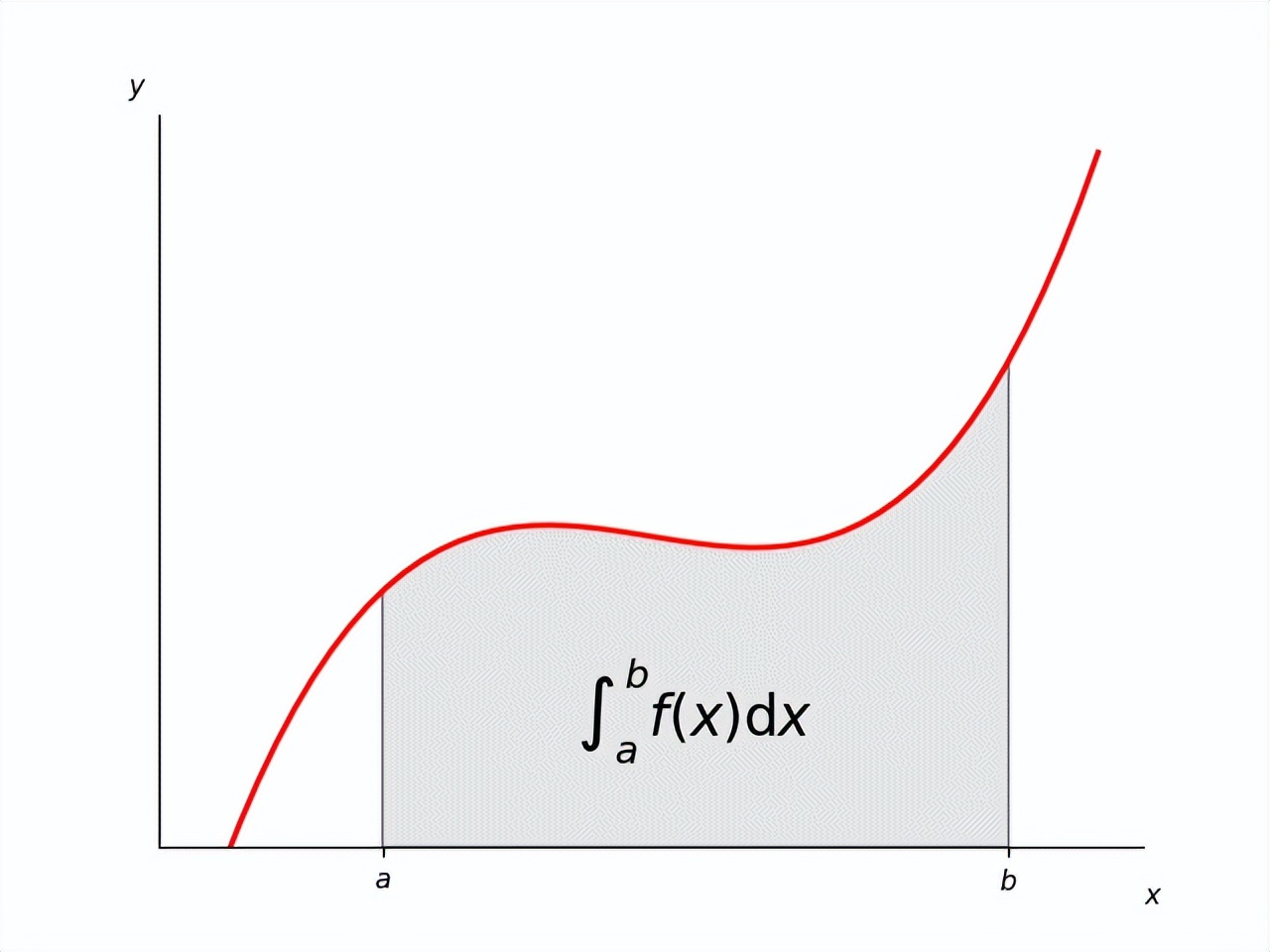
这公式啥意思呢?其实就是用来算围成曲边图形的面积的:
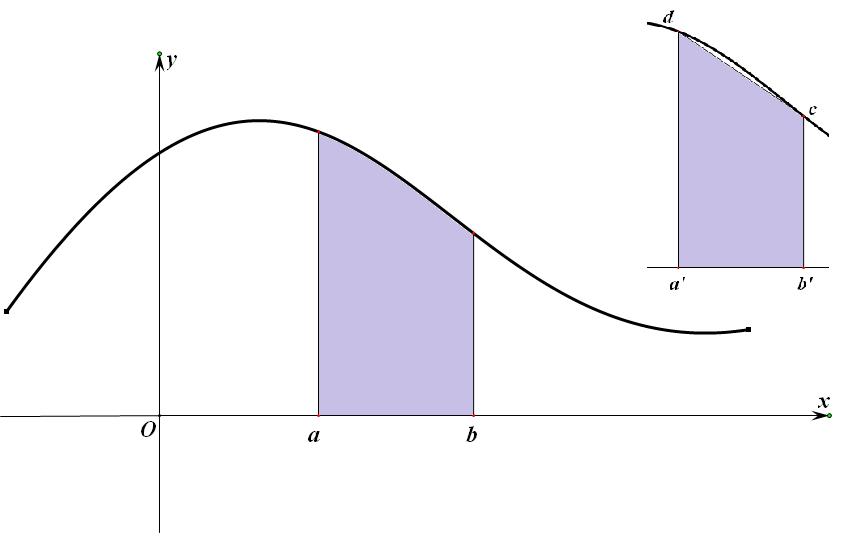
接着,我立刻做个数学实验,你马上就明白怎么操作的了:
我们还是请出抛物线y=x^2来:
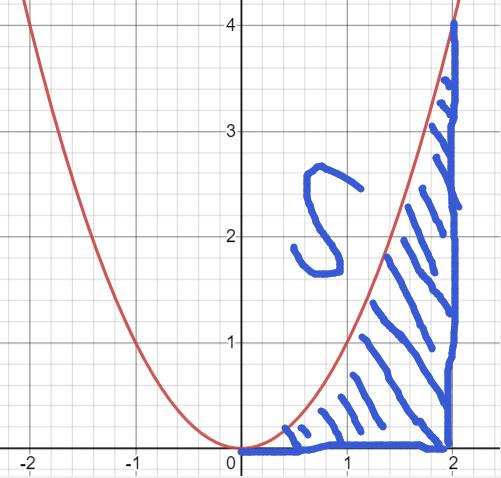
如何求图中的蓝色阴影部分的面积呢?(注意,它是由x=2,x轴,和抛物线共同围成的)
我们带入上面那个公式:
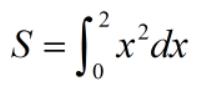
注意到:
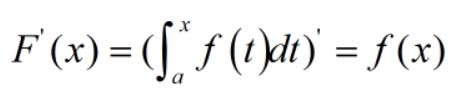
t和x是一个东西,只是换了个写法
我们要去寻找一个东西:究竟哪个函数求一下导是x^2呢?于是,我们翻出来微积分的书来查(或者上网去查),发现
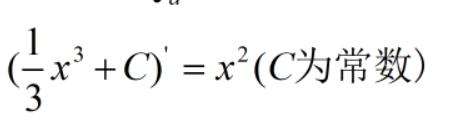
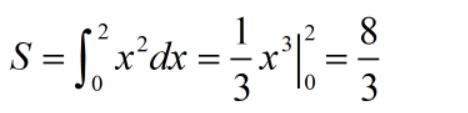
这里给大家分享一些微积分的基本公式,大家可以自己试着去积分一些简单曲边图形的面积:

还有一种方法是原始的定义法,但是笔者并不建议初学者使用,虽然它蕴含着微积分的思想,但几乎无法在实际中算面积:
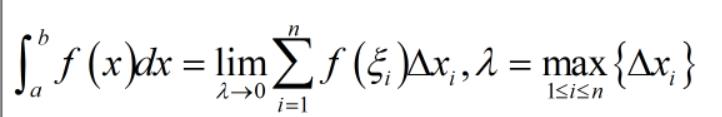
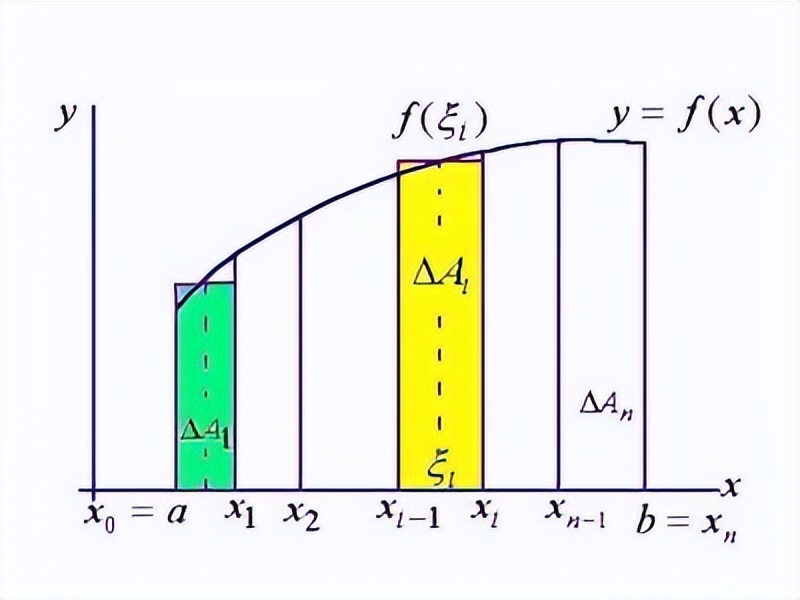
把所有的小面积加起来,就是总的面积
这种算法非常复杂,大家有兴趣可以自己研究一下。
最后,我们说一说定积分的物理意义,实际上,积分在大自然中无处不在,我们就简单举两个例子吧:
一是物体速率,距离和时间的关系:

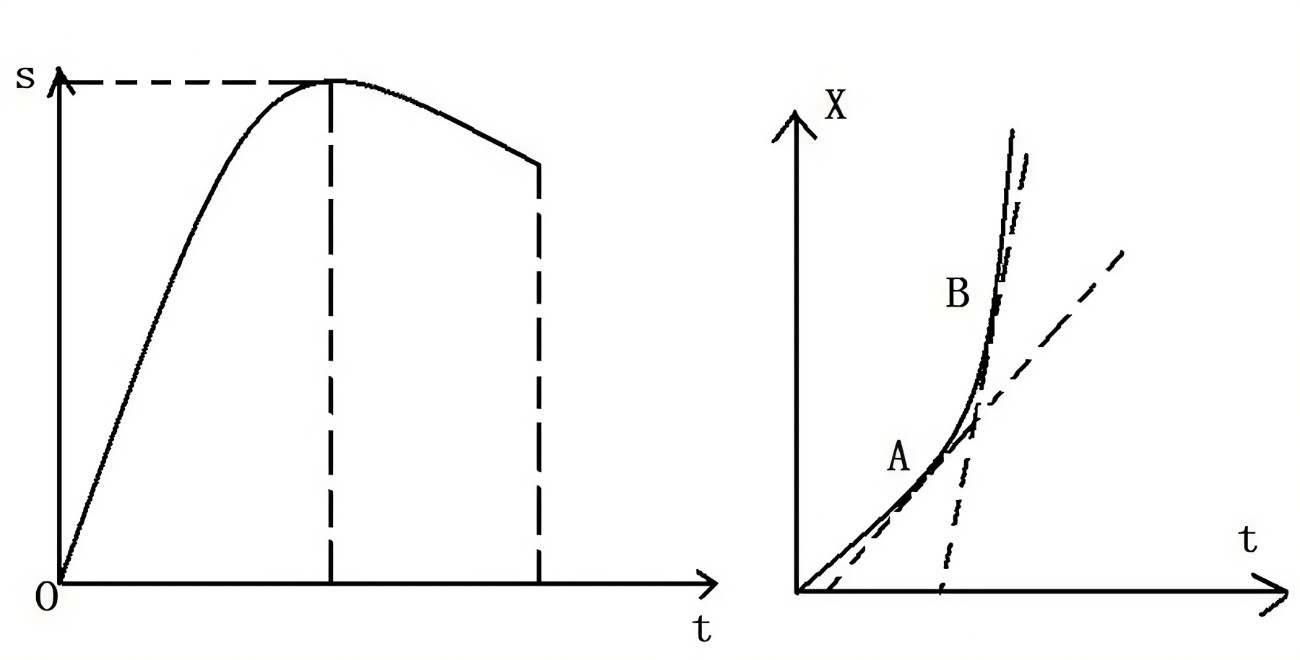
变速运动怎么用定积分描述呢?

二是电子器件的发热能量等于电流的平方乘以电阻,然后对时间进行积分:
定积分的入门笔者就讲到这里了,感谢大家抽空阅读,笔者写作的意义就在于激发大家的探索欲望,而不是仅交给大家光秃秃的知识,与其授之以鱼,不如授之以渔~