
1、基本积分表
(1)
(2)
(3)
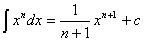
(4)
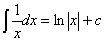
(5)
(6)
(7)
(8)
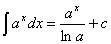
2、运算公式
(1)
(2)
(3)
3、
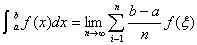
例1、若曲线 在x处的导数为
在x处的导数为 且曲线经过点A(1,3),求
且曲线经过点A(1,3),求 解析式。
解析式。
解: ,过A ∴
,过A ∴ ∴
∴
例2、求下列不定积分。
(1)
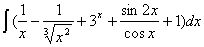
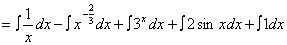
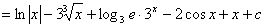
(2)
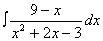
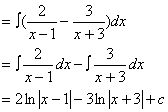
例3、求下列定积分
(1)
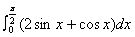
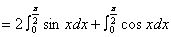
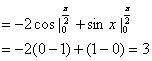
(2)
∵
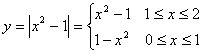
∴ 
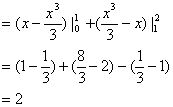
例4、 ,
, 为何值时,M最小。
为何值时,M最小。
解:
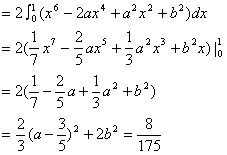
∴
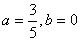
时,
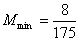
例5、已知 ,
, ,试求
,试求 的取值范围。
的取值范围。
解:
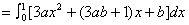
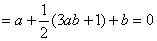
即
设 ∴
∴ 为方程
为方程
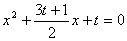
两根
 ∴
∴ 或
或
∴
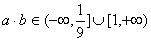
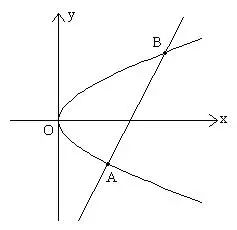
例6、求抛物线 与直线
与直线 所围成的图形的面积。
所围成的图形的面积。
解:由
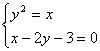
∴ A(1,-1)B(9,3)
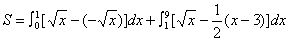
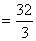
例7、求由抛物线 ,
, 所围成图形的面积。
所围成图形的面积。
解:
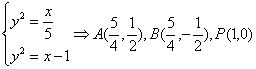
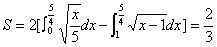
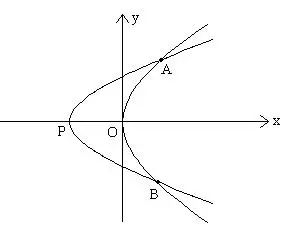
例8、由抛物线 及其在点A(0,-3),B(3,0)处两切线所围成图形的面积。
及其在点A(0,-3),B(3,0)处两切线所围成图形的面积。
解: ,
, ∴ P(
∴ P( )
)
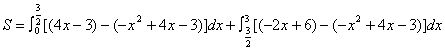
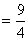
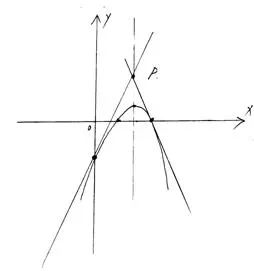
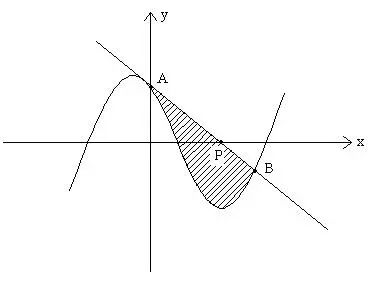
例9、曲线C: ,点
,点 ,求过P的切线
,求过P的切线 与C围成的图形的面积。
与C围成的图形的面积。
解:设切点 ,则
,则
切线: 过P(
过P( )
)
∴
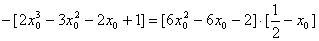

∴  A(0,1)
A(0,1)
∵  ∴
∴
∴
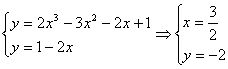
B(

)
∴
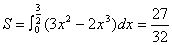
例10、抛物线 在第一象限内与直线
在第一象限内与直线 相切。此抛物线与x轴所围成的图形的面积记为S。求使S达到最大值的a,b值,并求
相切。此抛物线与x轴所围成的图形的面积记为S。求使S达到最大值的a,b值,并求 。
。
解:依题设可知抛物线为凸形,它与x轴的交点的横坐标分别为 ,所以
,所以 (1)
(1)
又直线 与抛物线相切,即它们有唯一的公共点
与抛物线相切,即它们有唯一的公共点
由方程组
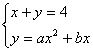
得 ,其判别式必须为0,即
,其判别式必须为0,即
于是
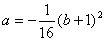
,代入(1)式得:
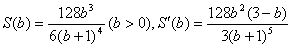
令 ;在
;在 时得唯一驻点
时得唯一驻点 ,且当
,且当 时,
时, ;当
;当 时,
时, 。故在时,
。故在时, 取得极大值,也是最大值,即
取得极大值,也是最大值,即 时,S取得最大值,且
时,S取得最大值,且
--END--


