探究三个“二次”函数的图像与性质特征
三个“二次”指的是二次函数、二次方程和二次不等式。它们的图像与性质分别如下：
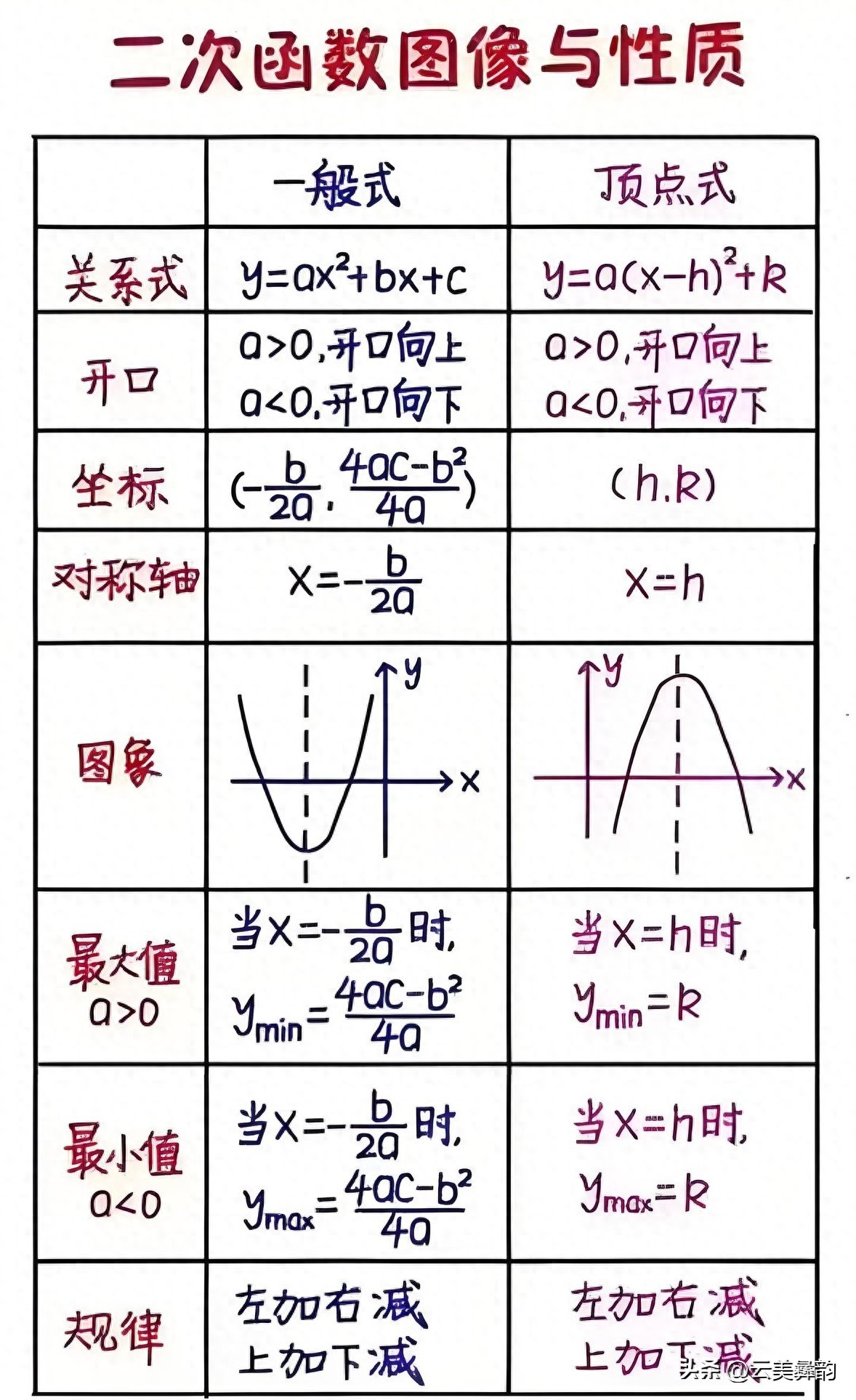
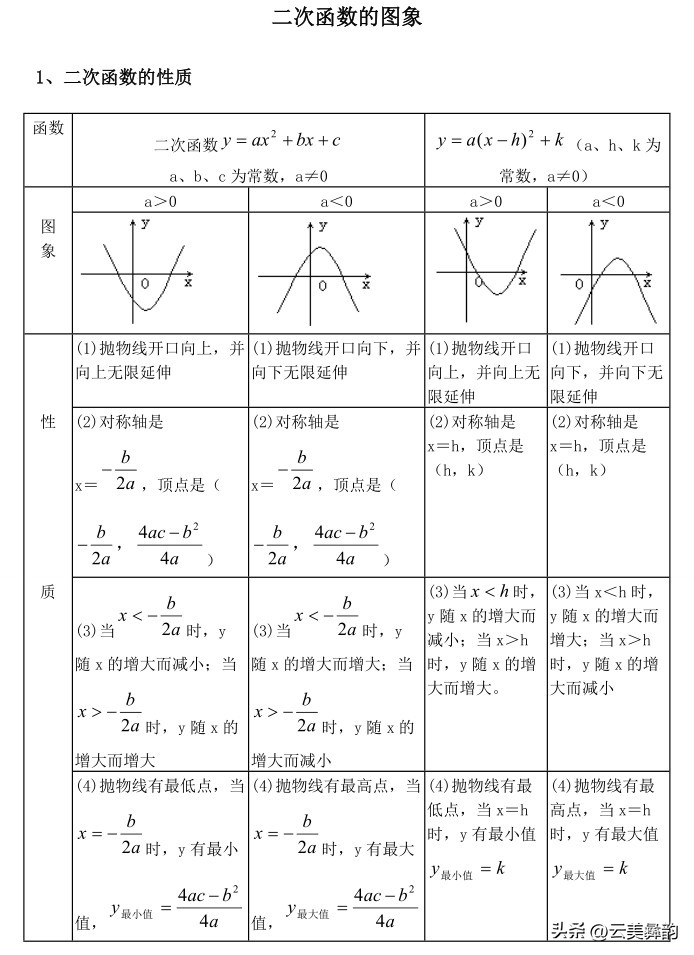
1. 二次函数：y = ax^2 + bx + c (a ≠ 0)
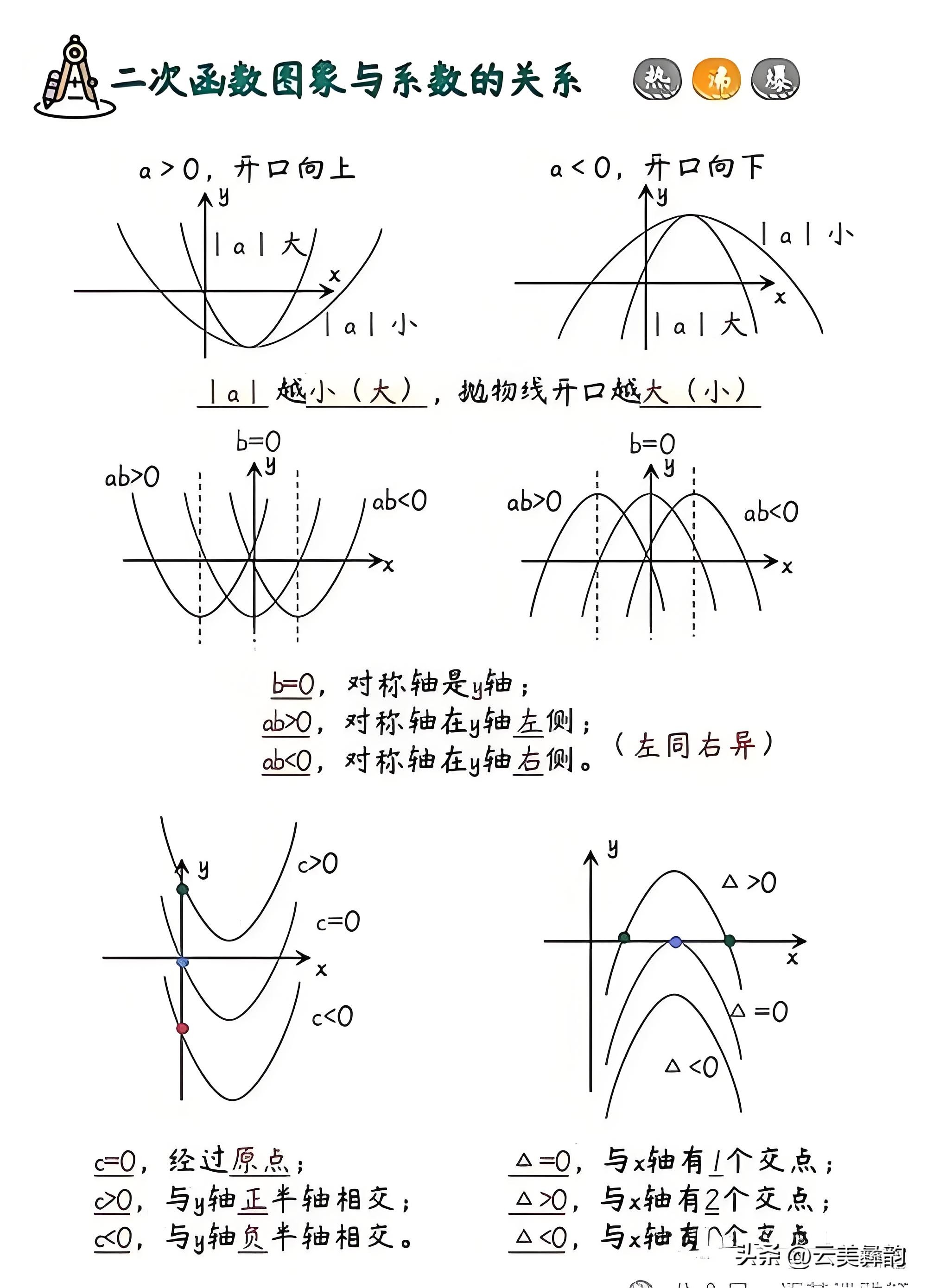
- 图像：抛物线。当a > 0时，开口向上；当a < 0时，开口向下。
- 性质：
- 对称轴：x = -b/(2a)
- 顶点：(-b/(2a), f(-b/(2a)))
- 最值：当a > 0时，有最小值f(-b/(2a))；当a < 0时，有最大值f(-b/(2a))
- 增减性：当a > 0时，在对称轴左侧单调递减，右侧单调递增；当a < 0时，在对称轴左侧单调递增，右侧单调递减
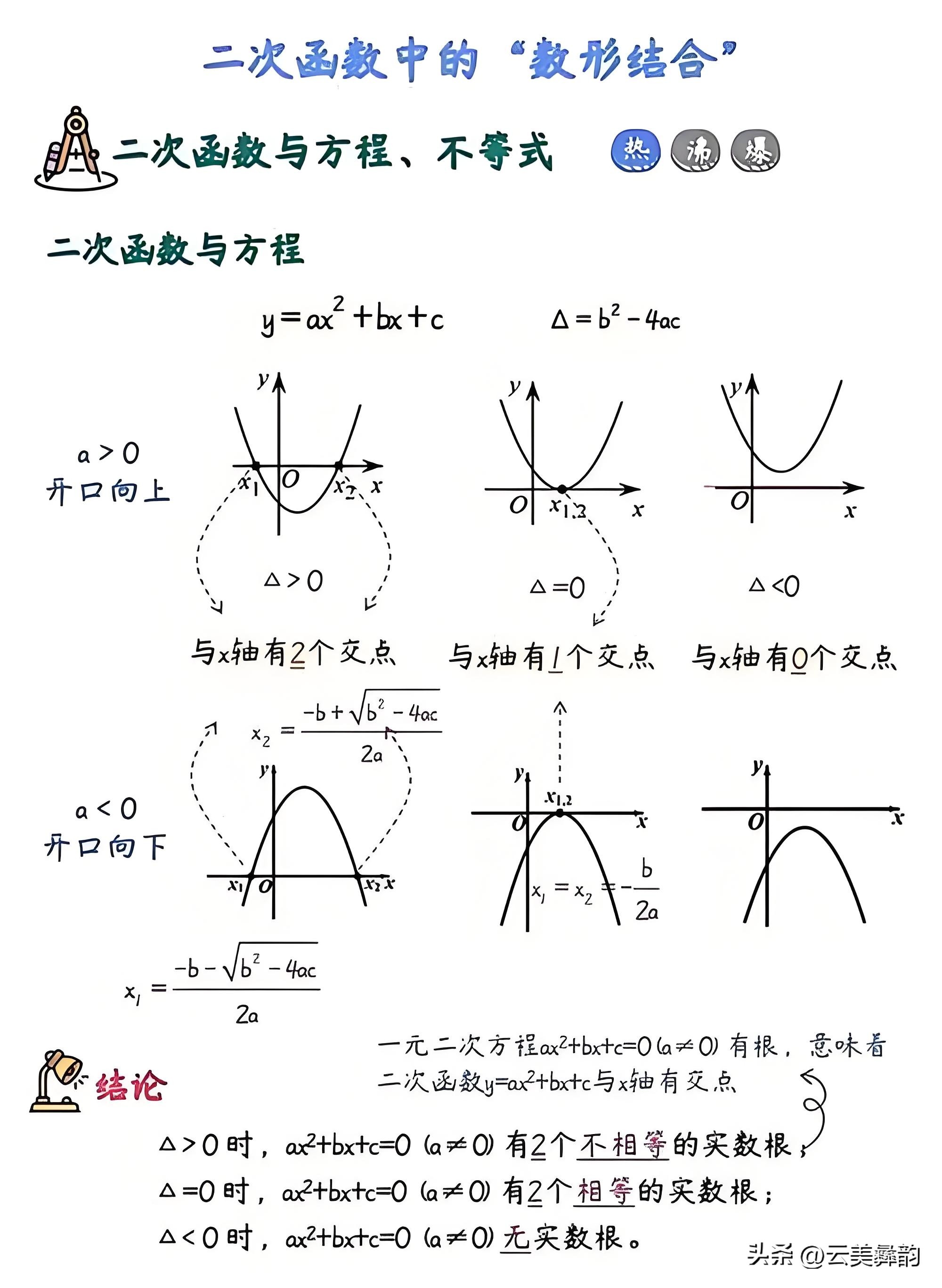
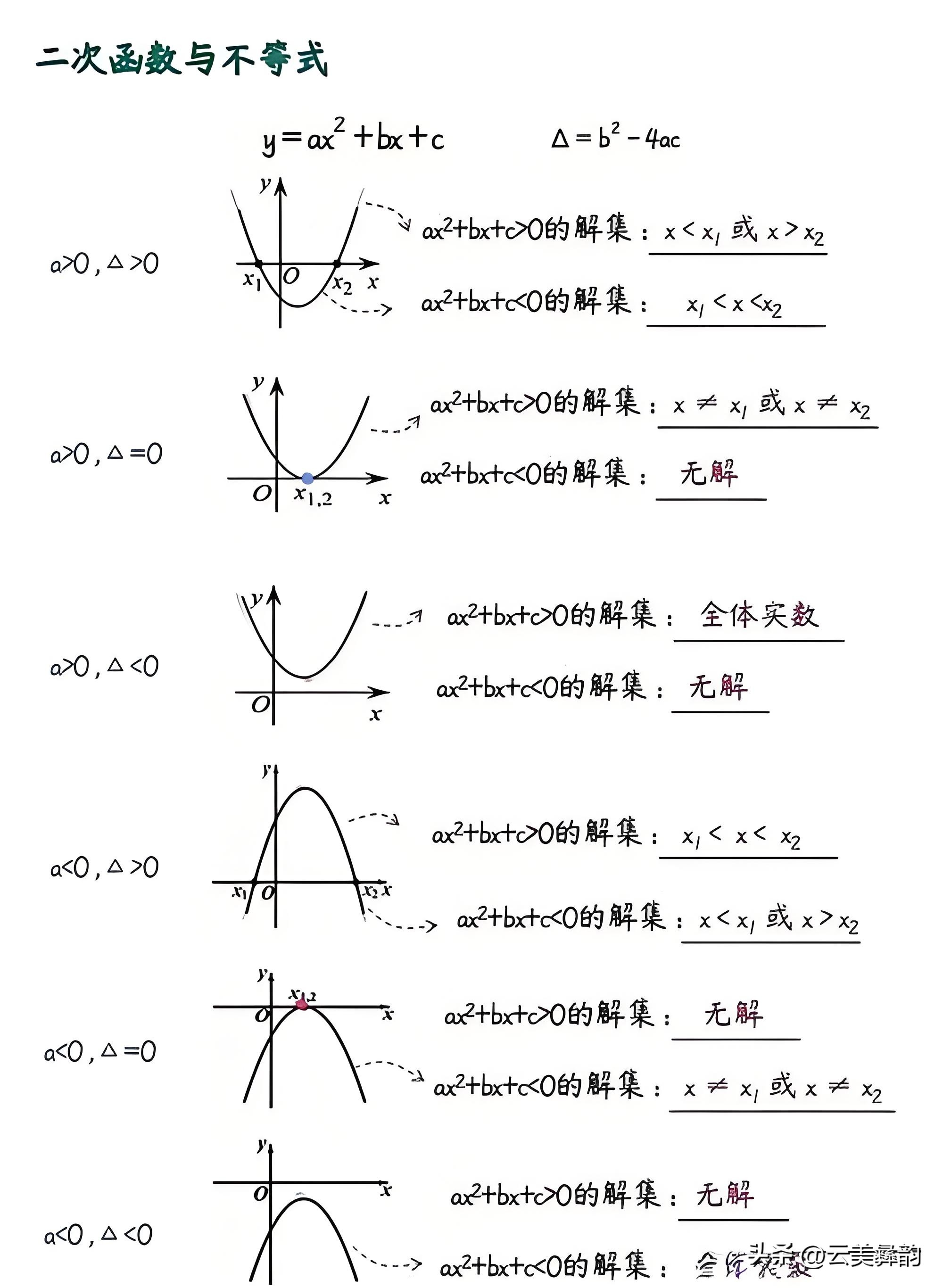
2. 二次方程：ax^2 + bx + c = 0 (a ≠ 0)
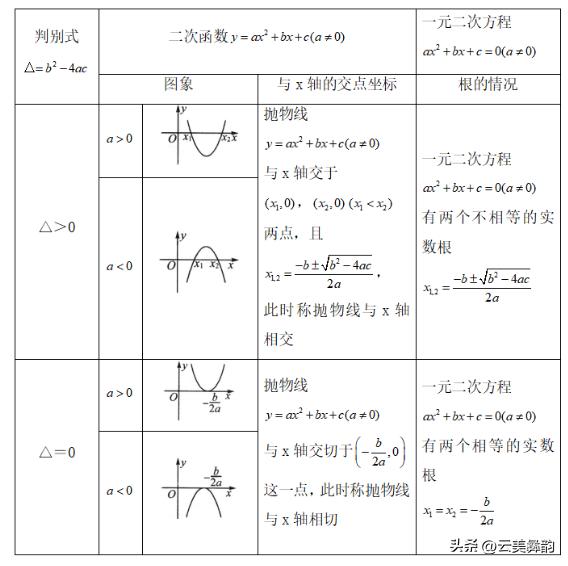
- 图像：与x轴的交点。如果方程有实数根，则图像与x轴有交点；如果没有实数根，则图像与x轴没有交点。
- 性质：
- 根的判别式：Δ = b^2 - 4ac
- 当Δ > 0时，方程有两个不相等的
相关内容：
1